 Verschiedene elliptische Kurven (Bild © )
Verschiedene elliptische Kurven (Bild © )
Einleitung
Heutzutage werden Gruppen auf der Basis von elliptischen Kurven in den meisten asymmetrischen Sicherheitsprotokollen neben den endlichen Körpern eingesetzt. Das Schlüsselvereinbarungsprotokoll Dragonfly -- das Herzstück von WPA3 –- ist keine Ausnahme: das Sicherheitsprotokoll stützt sich auf die Kryptographie elliptischer Kurven (engl. Elliptic Curve Cryptography, ECC) zur Herleitung von Schlüsseln aus Passwörtern. Die Fähigkeit, sich in den Bedeutungen der Zeichen, Elemente und Gleichungen elliptischer Kurven zurechtzufinden, ist für das Verständnis der Struktur und der Sicherheit des Protokolls unerlässlich. Aus diesem Grund wird die Einführung in die Theorie der elliptischen Kurven der Beschreibung der Protokollstruktur und der Erläuterung der WPA3-Angriffe vorangestellt.
Die Sicherheit eines Public-Key-Kryptosystems, dessen Basis elliptische Kurven darstellen, beruht auf einem rechnerisch schwer lösbaren Problem -- auf dem Diskreter-Logarithmus-Problem (engl. Discrete Logarithm Problem, DLP). Das Problem des diskreten Logarithmus über elliptische Kurven (engl. Elliptic Curve Discrete Logarithm Problem, ECDLP) ist derzeit schwieriger als die Faktorisierung ganzer Zahlen oder die Berechnung von diskreten Logarithmen in der multiplikativen Gruppe eines endlichen Körpers [1, §1]. ECC stammt aus den 1980er-Jahren, wobei solche bekannten Verfahren wie RSA oder Diffie-Hellman-Schlüsselaustausch (DHKE) mit den entsprechenden Problemen bereits in 1970er-Jahren zum Einsatz kamen [2, §9].
Abbildung 1: RSA- (oben) und ECC-Schlüssel (unten) für das AES-Sicherheitsniveau 128 Bit gegenübergestellt
ECC implementiert alle wichtigen Sicherheitstechniken der asymmetrischen Kryptosysteme: Verschlüsselung, Signierung und Schlüsselvereinbarung. Elliptische Kurven können in nahezu allen Protokollen eingesetzt werden, die auf DLP beruhen. Die Schlüsselgrößen von ECDLP-Verfahren, im Vergleich zu Kryptosystemen, die bspw. auf dem Faktorisierungsproblem (1) basieren, bei gleichem Sicherheitsniveau deutlich kürzer, wie die Abbildung 1 veranschaulicht. Allerdings ist die Verifikation von RSA-Signaturen mit kurzen Exponenten deutlich schneller als ECC [2, §9].
(1) Das Faktorisierungsproblem basiert auf der Schwierigkeit, große ganze Zahlen zu faktorisieren, also in Primfaktoren zu zerlegen [2, §8]. Dieses Problem wird z. B. im RSA-Verfahren eingesetzt.
Vergleicht man Schlüsselgrößen, die in DLP- und ECDLP-Verfahren eingesetzt werden, unterscheiden sich diese um ein Vielfaches, wie in Tabelle 1 ersichtlich ist.
| DLP & RSA | ECDLP | Verhältnis | Symmetrisch | Periode |
|---|---|---|---|---|
| 1024 Bit | 163 Bit | 1:6 | 80 Bit | Legacy |
| 2048 Bit | 224 Bit | 1:9 | 112 Bit | bis 2030 |
| 3072 Bit | 256 Bit | 1:12 | 128 Bit | > 2030 |
| 7680 Bit | 384 Bit | 1:20 | 192 Bit | > 2030 |
| 15360 Bit | 512 Bit | 1:30 | 256 Bit | > 2030 |
Tabelle 1: Vergleich von Schlüsselgrößen der DLP-/RSA- und ECDLP-Verfahren. Die dritte Spalte stellt das Verhältnis DLP/RSA zu ECDLP in Bezug auf die Schlüssellängen dar [3]
ECC-Kryptoalgorithmen können verschiedene zugrunde liegende elliptische Kurven verwenden. Unterschiedliche Kurven bieten unterschiedliche kryptografische Sicherheitsniveaus, unterschiedliche Leistung (Geschwindigkeit) und unterschiedliche Schlüssellänge.
Zu den Bestandteilen der ECC-Kurven, die in den gängigen kryptografischen Bibliotheken und Sicherheitsstandards verwendet werden, gehören:
- Bezeichnung, z. B. "secp256k1" oder "Curve25519",
- endlicher Körper, dessen Größe die Schlüssellänge definiert, z.B. 256 Bit,
- Gleichung bzw. Gleichungsparameter, die die Kurve selbst definieren,
- Sicherheitsstärke, die normalerweise der Hälfte der Körpergröße entspricht,
- Leistung (Operationen pro Sekunde) und andere Parameter.
Mathematische Grundlagen
Die im Abschnitt verwendete Notation lehnt sich an die in der technischen Richtlinie von BSI zu den elliptischen Kurven verwendete [1, §1.3].
In der Mathematik sind elliptische Kurven ebene algebraische Kurven, bestehend aus allen Punkten ${x, y}$, beschrieben durch die Gleichung [4]:
$$ Ax^3+Bx^2y+Cxy^2+Dy^3+Ex^2+Fxy+Gy^2+Hx+Iy+J=0. $$
Hierbei werden Elemente $A,B,...,J$ aus einem Körper $K$ genommen. Als $K$ wird eine Menge komplexer, reeller, rationaler Zahlen oder ein endlicher Körper eingesetzt. Die Kryptographie verwendent diese Kurven in vereinfachter Form:
$$ y^2=x^3+ax+b, $$
wobei $a,b \in K$. Diese Form heißt Weierstraß-Form und lässt sich nur unter strikten Bedingungen aus der allgemeinen Form bilden.
Es sei betont, dass in Kryptosystemen die Berechnungen nicht in der Menge der reellen Zahlen erfolgen, sondern in einem endlichen Körper modulo Primzahl. Das folgende Beispiel ist vereinfacht und wird in nachfolgenden Kapiteln verfeinert. Damit soll das erste allgemeine Verständnis der elliptischen Kurven verschafft werden.
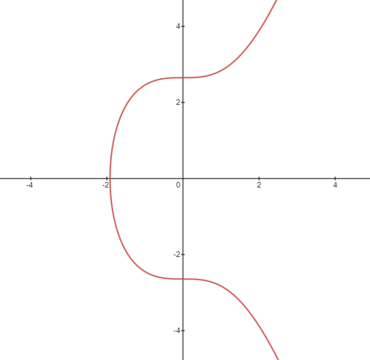
Als Beispiel dient die Kurve "secp256k1", die im Bitcoin-Kryptosystem zum Einsatz kommt und vom Konsortium Standards for Efficient Cryptography Group (SECG) definiert wird [5]. In den reellen Zahlen hat die Kurve die folgende Gleichung:
$$ y^2 = x^3 + 7, $$
Die Gleichung lässt sich konstruieren, indem man $a=0$ und $b=7$ in die generischen Weierstraß-Form einsetzt.
Abbildung 2: Darstellung der Kurve secp256k1 im kartesischen Koordinatensystem in reellen Zahlen
Diese Kurve wird im Bitcoin-Kryptosystem bei dem digitalen Signaturalgorithmus auf elliptischen Kurven (engl. Elliptic Curve Digital Signature Algorithm, ECDSA) verwendet Mit diesem Algorithmus kann eine Transaktion (2) signiert und verifiziert werden. Graphisch ist die Kurve in der Abbildung 2 dargestellt.
(2) Eine Transaktion ist der Transfer eines Betrages zwischen Bitcoin-Wallets [6].
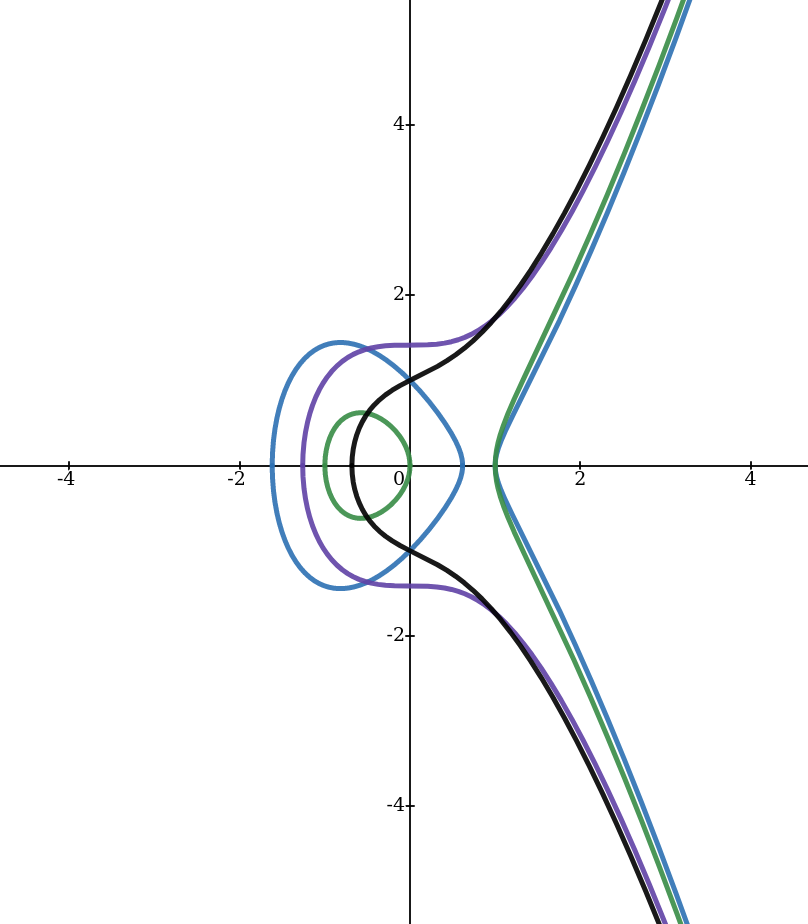
Dabei unterscheiden sich die Formen einer Weierstraß-Kurve abhängig von den gewählten Parametern $a$ und $b$. Verschiedene Formen sind in der Abbildung 3 zu sehen.
Abbildung 3: Parameterwerte und die damit definierten elliptischen Kurven im kartesischen Koordinatensystem in reellen Zahlen [7]
Nicht alle elliptischen Kurven sind für die Zwecke der Kryptographie geeignet. Sichere Kurven werden von Experten ausgewählt, veröffentlicht und standardisiert. Darüber hinaus repräsentiert die Weierstraß-Gleichung bspw. für den Fall $(a,b)=(0,0)$ keine elliptische Kurve, da die Parameterwerte eine singuläre Kurve bilden. Solche Kurven dürfen in Kryptosystemen nicht verwendet werden, denn diese sind leicht angreifbar [8; 9].
Gruppe als algebraische Struktur
Bevor die allgemeine Definition gegeben werden kann, müssen die Grundlagen der Gruppentheorie verinnerlicht werden. Die Gruppentheorie als mathematische Disziplin beschäftigt sich mit algebraischen Strukturen (Mengen), die strikte Eigenschaften und eine klar definierte zweistellige Verknüpfung besitzt. Die Verknüpfung legt fest, wie die Elemente unter der Berücksichtigung der Eigenschaften miteinander verbindet werden und wie ein neues Element daraus generiert wird [10, §2.1.1].
Eine Gruppe ist eine Menge $G$ mit einer inneren Verknüpfung $\circ:G \times G \rightarrow G$ (abgeschlossen). Diese Verknüpfung muss die folgenden drei Eigenschaften besitzen [10, §2.1.1]:
- Assoziativität der Elemente,
- Existenz eines neutralen Elements und
- Invertierbarkeit jedes Elements.
Dabei ist eine Gruppe abelsch, wenn in dieser auch das Kommutativgesetzt für ihre Elemente gilt. ECC-Kryptosysteme setzen voraus, dass jede von diesen Eigenschaften in der Gruppe, die als Basis eines Kryptosystems dient, vertreten werden muss.
Anschließend sind die Notationen einzuführen. Die Verknüpfung $\circ$ wird i.d.R. nicht direkt verwendet, sondern entweder durch das Pluszeichen ($+$) oder durch das Multiplikationszeichen ($\cdot$) ersetzt. Es ist dabei von Bedeutung, wie man die Verknüpfung einer beliebigen Anzahl von Elementen darstellen kann [1, §2.2.1].
Für die additive Notation wird $0$ als neutrales Element verwendet, das Inverse wird mit $-g,g\in G$, bezeichnet. Dabei spielt die Summe mehrerer Gruppenelemente eine wichtige Rolle. Diese wird mit $[k]g$ bezeichnet und folgendermaßen definiert:
$$ [k]g=\sum^k_1g, k\in \mathbb{N}. $$
Die multiplikative Notation gibt $1$ als neutrales und $g^{-1},g\in G$ als inverses Element vor. Das Produkt $g^k$ wird in diesem Fall wie folgt definiert:
$$ g^k=\prod^k_1g, k\in \mathbb{N}. $$
In den nächsten Kapiteln wird es tiefer in die auf der Gruppendefinition aufbauenden Begriffe eingestiegen.
Ordnung einer Gruppe
Sei $G$ eine endliche Gruppe (3), wobei die Elementanzahl gleich $n$ ist. Diese Anzahl $n$ wird Gruppenordnung genannt und als $\text{#}G$ bezeichnet [1, §2.2.2]. Da $G$ eine endliche Gruppe ist, existiert für jedes Element $g$ der Gruppe so eine Zahl $k$, $1\leq k \leq n$, dass $[k]g=0$. Ein kurzer Beweis für diese Behauptung ist unten im Appendix zu finden. Grundsätzlich folgt diese Eigenschaft aus dem kleinen Satz von Fermat (vgl. [10, Satz 3.11]).
(3) Eine endliche Gruppe enthält eine abzählbare, also eine begrenzte Anzahl von Elementen.
Generator
Eine endliche Gruppe $(G,+)$ der Ordnung $n$ ist zyklisch, wenn ein Element $g\in G$ existiert, so dass gilt
$$ G={g,[2]g,[3]g,...,[n-1]g,[n]g}. $$
Wie es zu sehen ist, lässt sich die komplette Gruppe $G$ nur aus dem Element $g$ generieren. Das neutrale Element wird dabei durch eines der Elemente $[k]g$, $1 \leq k \leq n$, vertreten. Das Element $g$ wird daher als Generator bezeichnet [1, §2.2.2].
Wenn eine Gruppe zyklisch ist, beinhaltet diese ein Generator-Element. Dass bedeutet allerdings nicht, dass jedes Element unbedingt ein Generator ist. Dafür muss dieses relativ prim zur Ordnung der Gruppe sein. Damit jedes Element einer Gruppe, bis auf das neutrale, die komplette Gruppe generieren kann, muss die Ordnung dieser Gruppe prim sein [2, Satz 8.4].
Untergruppe
Sei $G$ eine endliche Gruppe. Dann wird eine Untermenge $S$ eine Untergruppe genannt, wenn $S \subseteq G$ gilt und $S$ mit $\circ$ eine Gruppe bildet [11].
Mit dieser Definition lässt sich eine Eigenschaft jeder endlichen Gruppe einführen: Jedes Element $s\in G$ generiert eine zyklische Untergruppe von $G$, mit allen dazugehörigen Eigenschaften. Die Eigenschaft kann wie folgt beschrieben werden [1, §2.2.3]:
$$ \forall s\in G \ \exists \langle s \rangle \subseteq G: \langle s \rangle = {[k]s: 1\leq k \leq \text{ #}s}. $$
Die Zahl $\text{#}s$ steht für die Ordnung des Elements $s$ der Gruppe $G$ und entspricht der Größe der Untergruppe $\langle s \rangle$.
Endlicher Körper
Ein Körper ist eine Menge von Zahlen $F$, die mit zwei Verknüpfungen, $+$ und $\cdot$, eine abelsche Gruppen bildet. Ein Körper wird durch vier Eigenschaften definiert [1, §2.2.4]:
- $+$ und $\cdot$ sind abgeschlossen $(+:F \times F \rightarrow F$ und $\cdot:F \times F \rightarrow F$),
- $(F,+)$ ist eine additive abelsche Gruppe,
- $(F\setminus{0},\cdot)$ ist eine multiplikative abelsche Gruppe,
- für $a,b,c\in F$ gilt $(a+b)\cdot c = a\cdot c + b\cdot c$.
Ein endlicher Körper ist ein Körper mit endlich vielen Elementen. Dabei ist es erwähnenswert, dass ein endlicher Körper mit $q$ Elementen dann und nur dann existiert, wenn es eine Primzahl $p$ gibt, so dass $q=p^r$ für $r\geq1$. Ein solcher endlicher Körper heißt Primkörper und wird als $\mathbb{F}_q$ bezeichnet. Häufig wird der Fall $r=1$ verwendet -- $\mathbb{F}_p$. Dazu ist es zu betonen, dass sowohl die additive als auch die multiplikative abelsche Gruppe eines Primkörpers zyklisch ist [12]. Da ein Primkörper zu $(\mathbb{Z}_p,+,\cdot)$ isomorph (4) ist, wird $\mathbb{F}_p$ hier einfachheitshalber als Menge von ganzen Zahlen ${0,1,...,p-1}$ mit den dazugehörigen Gruppenverknüpfungen betrachtet.
(4) Zwei algebraische Strukturen sind isomorph, wenn Elemente einer Struktur auf die Elemente der anderen eindeutig abgebildet werden können und umgekehrt. Isomorphe Strukturen sind austauschbar. Das heißt, Ergebnisse der Operationen mit den Strukturen bleiben nach einem Austausch der Strukturen unverändert [13].
Elliptische Kurven über endliche Körper
Auf elliptischen Kurven basierende Kryptosysteme verwenden i.d.R. elliptische Kurven über dem endlichen Körper $\mathbb{F}_p$, wobei $p>3$. Das bedeutet, dass die Definitions- und die Wertemenge einer Kurve der Menge aller ganzen Zahlen im Intervall $[0,p-1]$ entsprechen. Damit lässt sich eine elliptische Kurve über einen Primkörper als eine Funktion der Form $\mathbb{F}_p \rightarrow \mathbb{F}_p$ darstellen. Um die Abgeschlossenheit der Gruppenverknüpfung zu gewährleisten, wird es modulo $p$ gerechnet.
Im Gegensatz zum RSA-Verfahren, bei dem man mit den ganzen Zahlen arbeitet, interessiert sich ECC für die Menge aller Punkte einer elliptischen Kurve $E$ und für die möglichen Verknüpfungen der Punkten. Die Tatsache, dass über die Menge der Punkte einer elliptischen Kurve eine Gruppe $G(E)$ gebildet wird, spielt dabei die ausschlaggebende Rolle. Für kryptographische Zwecke wird die Gruppe $G(E)$ allerdings nicht komplett betrachtet, sondert auf die Menge von Punkten $E(\mathbb{F}_p)$ reduziert. $E(\mathbb{F}_p)$ stellt eine Untergruppe von $G(E)$ dar. Genauer gesagt, entsprechen Punkte aus $E(\mathbb{F}_p)$ den Punkten, die gleichzeitig auf der Kurve $E$ liegen und zu $\mathbb{F}_p^2$ gehören (5). Außerdem wird dieser Untergruppe ein besonderer Punkt zugeordnet -- der Punkt im Unendlichen. Gruppen der Form $E(\mathbb{F}_p)$ sind Gruppen elliptischer Kurven modulo Primzahl (engl. Elliptic Curve groups over a Prime field, ECP).
(5) Mit $\mathbb{F}_p^2$ wird ein kartesisches Produkt der Form $\mathbb{F}_p \times \mathbb{F}_p$ bezeichnet, das nichts anderes als eine Menge von Wertepaaren ist, z.B. $(x,y)$, wobei $x,y \in \mathbb{F}_p$. Das heißt, jede Koordinate muss eine ganze Zahl im Bereich $[0,p-1]$ sein.
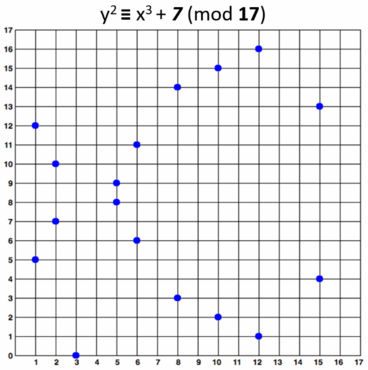
Da eine endliche Menge von Punkten einer elliptischen Kurve betrachtet wird, hätte die Kurve secp256k1 im Raum der reellen Zahlen eine entfernte Ähnlichkeit mit der Kurve in der Abbildung 4.
Abbildung 4: Punktgruppe $E(\mathbb{F}_{17})$ der Kurve secp256k1 im kartesischen Koordinatensystem [14]
Die dargestellte Kurve wird nicht in der Praxis eingesetzt, da eine kleine Primzahl $17$ keine Sicherheit gewährleistet. In der Praxis werden große Primzahlen ausgewählt, sodass die Punktverteilung nach einer zufälligen Punktwolke aussieht.
Definition einer elliptischen Kurve über Primkörper
In diesem Kapitel wird die Gruppe $E(\mathbb{F}_p)$ genauer definiert. Als Erstes wird die allgemeine Gleichung einer elliptischen Kurve über Primkörper angeführt. Eine elliptische Kurve $E$ über $\mathbb{F}_p$, $p>3$ (6), ist eine Menge der Punkte $(x,y)$ mit $x,y \in \mathbb{F}_p$, die die folgende Gleichung erfüllen [2, Definition 9.1]:
$$ y^2 \equiv x^3 + ax + b \text{ mod } p, $$
wobei $a,b\in \mathbb{F}_p$ und die Bedingung $4a^3+27b^2 \neq 0 \text{ mod } p$ gilt (7). Zu der elliptischen Kurve gehört des Weiteren auch der imaginäre Punkt im Unendlichen $\mathcal{O}$.
(6): Ohne die Bedingung $p > 3$ könnte man die allgemeine Gleichung der elliptischen Kurven nicht vereinfachen, um die Weierstraßform zu bekommen [1, §2.3.1].
(7): Da die Diskriminante ungleich null ist, werden sogenannte Singularitäten ausgeschlossen. Andernfalls gäbe es Punkte, deren Tangente nicht existiert oder nicht wohldefiniert (nicht eindeutig) ist. Letzteres ist aber für das Rechnen auf elliptischen Kurven erforderlich [2, §9.1.1]. Für Zusatzinformationen s. [15].
Die Gruppe $E(\mathbb{F}_p)$ wird damit wie folgt definiert [1, Gleichung 2.6]:
$$ E(\mathbb{F}_p)={(x,y)\in \mathbb{F}_p^2:y^2=x^3+ax+b \text{ mod } p}\text{ } \cup \text{ }{\mathcal{O}} $$
Verknüpfung der Punkte einer elliptischen Kurve
Für eine jede Gruppe muss eine Verknüpfung definiert werden. Im Falle der Gruppe $E(\mathbb{F}_p)$ heißt diese "Addition" oder "Punktaddition" und wird als $+$ bezeichnet. Wie der Name schon sagt, werden zwei Punkte verknüpft, nicht Zahlen. Die Bezeichnung des Gruppengesetzes kann irreführend sein, da die Punkte nicht koordinatenweise, wie üblich, addiert werden. Die Operation "Addition" ist kompliziert und nicht intuitiv nachvollziehbar. Zur Erklärung der Auswahl der Gruppengesetzbezeichnung wird die Aussage von C. Paar und J. Pelzl im Buch "Kryptographie verständlich" verwiesen:
"Man beachte, dass die Bezeichnung der Gruppenoperation als Addition rein willkürlich ist. Man hätte sie ebenso gut Multiplikation nennen können" [2, §9.1.2].
Es sei erwähnt, dass bspw. im RFC-Dokument zu den grundlegenden ECC-Algorithmen die multiplikative Notation verwendet wird, um die Konsistenz zu den älteren Publikationen zu behalten [16]. In diesem Artikel wird die additive Notation verwendet.
Gegeben seien eine elliptische Kurve in der Weierstraßform $y^2 = x^3 + ax + b$ und zwei Punkte $P=(x_1, y_1)$ und $Q=(x_2, y_2)$, die auf der Kurve liegen, wobei $x_1 \neq x_2$. Bei der Verknüpfung zweier Punkte bekommt man einen dritten Punkt auf derselben elliptischen Kurve [2, §9.1.2]:
$$
P+Q=R
(x_1, y_1)+(x_2, y_2)=(x_3, y_3),
$$
wobei $R\in E$.
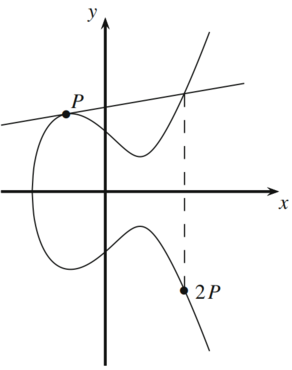
In der Kryptographie wird ein Sonderfall der Punktaddition verwendet -- die Punktverdopplung $P+P=2P$, wobei $2P\in E$. Diese Operation lässt sich geometrisch anschaulich darstellen (s. Abbildung 5). Es wird eine Tangente zur elliptischen Kurve durch den Punkt $P$ gezogen, und als Ergebnis wird die Spiegelung des resultierenden Schnittpunktes an der $x$-Achse genommen.
Abbildung 5: Geometrische Darstellung der Punktverdopplung [2, Abb. 9.5]
Diese Operation wird i.d.R. mehrmals wiederholt und nennt sich Skalarmultiplikation, wobei die Rolle des Gruppenelements ein Punkt $P$ auf der elliptischen Kurve spielt:
$$ [k]P=\sum^k_1P, k\in \mathbb{N}. $$
Es ist nicht intuitiv klar, warum die Addition auf diese Weise definiert wird. Die Natur des Gruppengesetzes hängt stark von der algebraischen Struktur ab, in der die Kurve definiert wird [17, Folie 33]. Die Punkte einer elliptischen Kurve mit Koordinaten in den komplexen Zahlen bilden einen Torus. Vereinfacht entspricht die Gruppenaddition in diesem Fall der (normalen) Modulo-Addition von komplexen Zahlen, die sich auf dem Torus befinden. Die Addition im Raum komplexer Zahlen entspricht im Grunde der Addition von Vektoren. Daher lässt sich die geometrische Interpretation der Vektorenaddition übernehmen (8).
(8) Die Addition zweier komplexen Zahlen ähnelt sich der Vektorenaddition und ist in der Abbildung zu sehen.
Um die Punktverdoppelung in einem Programm implementieren zu können, wird die Definition der Gruppenoperation in algebraischer Form verwendet. Um die Verknüpfung algebraisch zu definieren, sollen die Schnittpunkte der elliptischen Kurve und der Tangente gefunden werden (s. Abbildung 5 und Algorithmus in [18]). Dafür bildet man ein Gleichungssystem, dessen Lösung dem folgenden Punkt entspricht:
$$
x_2 \equiv s^2-2x_1 \text{ mod } p
y_2 \equiv s(x_1-x_2)-y_1 \text{ mod } p,
$$
wobei $s \equiv (3x_1^2+a) / (2y_1) \text{ mod } p$ der Steigung der Tangente entspricht, $(x_1,y_1)$ der Punkt ist, durch den die Tangente gezogen wird, und $(x_2,y_2)$ das Ergebnis der Punktverdopplung ist.
Punkt im Unendlichen und das inverse Element
Damit $E(\mathbb{F}_p)$ alle Gruppeneigenschaften besitzt, muss das neutrale Element definiert werden. Es gibt keinen Punkt in $E(\mathbb{F}_p)$, der die Rolle des neutralen Elements $e$ übernehmen und dabei die Gleichung $P+e=P$ mit $P\in E(\mathbb{F}_p)$ erfüllen könnte. Daher wird der Punkt im Unendlichen $\mathcal{O}$ definiert [2, §9.1.2]. Den Punkt im Unendlichen soll man sich so vorstellen, dass es sich um einen künstlichen Punkt der Kurve handelt, der eingeführt wurde, um "Lücken" in der Definition der Punktaddition zu beseitigen und als neutrales Element der Gruppe zu fungieren (9). Dieser kann als Punkt betrachtet werden, der sich gleichzeitig an beiden Enden (ganz oben und ganz unten im Unendlichen) aller Geraden befindet, die zur y-Achse parallel sind [19].
(9): Es sei vermerkt, dass der Punkt eine geometrische und algebraische Bedeutung im projektiven Koordinatiensysten hat [20; 21].
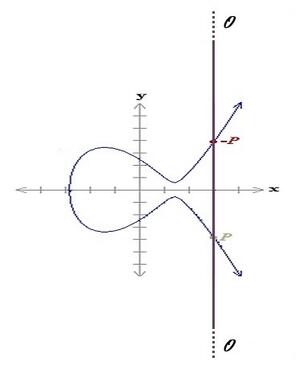
Mit dem Punkt im Unendlichen lässt sich die Inverse $-P$ definieren. Die Koordinaten des Punktes im Unendlichen unterscheiden sich von dem erwarteten $(0,0)$-Wert. Dieser Punkt hat im Grunde keine sinnvollen Koordinaten im affinen (bzw. kartesischen) Koordinatensystem, mit denen gerechnet werden könnte. Daher ist es einfacher, das inverse Element anhand einer graphischen Darstellung zu definieren. Die Abbildung @fig:infpoint dient zu Veranschaulichung des Ausdrucks $P+(-P)=\mathcal{O}$ im Raum der reellen Zahlen. Somit entspricht $-P$ dem Punkt $(x,-y)$ mit $P=(x,y)$. Da $E(\mathbb{F}_p)$ über einen Primkörper definiert wird und $-y\equiv 0 - y \equiv p-y \text{ mod } p$, hat die Inverse die Form $(x,p-y)$.
Abbildung 6: Punkt im Unendlichen als Ergebnis der Subtraktion eines Punktes von sich selbst im kartesischen Koordinatensystem in den reellen Zahlen [22]
Kofaktor
Wie im Abschnitt "Untergruppe" angesprochen, generiert jedes Element einer Gruppe eine zyklische Untergruppe. Dabei überschneiden sich diese Untergruppen nicht und bilden zusammen die komplette Gruppe. Es sei hervorgehoben, dass manche Untergruppen eine kleinere Ordnung als die anderen haben können, was bedeutet, dass diese eine kleinere Anzahl von Elementen haben. Dies kann vorkommen, wenn die Anzahl von Punkten in $E(\mathbb{F}_p)$ keine Primzahl ist. Nimmt man eine von Untergruppen $S$, so ist der Kofaktor in dem Fall $h=n/r$, wobei $r$ die Ordnung von $S$ und $n$ die Ordnung der Gruppe ist. Unabhängig davon, welche Untergruppe ausgewählt wird, ist $h$ eine natürliche Zahl (und nicht eine Rationale) nach dem Satz von Lagrange [2, Satz 8.6].
Ist die Ordnung der Gruppe prim, gibt es nur eine zyklische Untergruppe -- die Gruppe selbst, und $h=n/r=n/n=1$. Außerdem ist jeder Punkt außer $\mathcal{O}$ ein Generator.
Unterschiedliche Kurven haben unterschiedliche Kofaktoren:
- Curve25519 besitzt den Kofaktor von $8$,
- Curve448 -- den Kofaktor von $4$ und
- für secp256k1 ist die Punktanzahl prim, weswegen der Kofaktor einer $1$ entspricht.
Base Point
Für elliptische Kurven über endlichen Körpern definieren die ECC-Kryptosysteme einen speziellen (konstanten) Punkt namens Base Point, der in seiner Untergruppe als Generator fungiert. Der Kofaktor einer Gruppe hängt somit davon ab, welcher Base Point verwendet wird.
Für Kurven mit dem Kofaktor $1$ gibt es nur eine Untergruppe, und als Base Point kann aus dieser Sicht jeder Punkt genommen werden. In diesem Fall können alle Punkte auf der Kurve (einschließlich des Punktes im Unendlichen) mit dem Base Point erzeugt werden.
Ist der Kofaktor größer $1$, wird ein Base Point ausgewählt, der eine für die Zwecke eines kryptographischen Verfahrens geeignete Untergruppe erzeugt. Ein richtig gewählter Basispunkt gewährleistet die Effizienz der Berechnungen und die Sicherheit des Verfahrens. Erzeugt der gewählte Base Point eine kleine Untergruppe, ist das Kryptosystem möglicherweise gegen Small-Subgroup-Angriffe (10) anfällig [23, §3], da der Schlüsselraum von der Untergruppengröße abhängt.
(10) Es gibt mehrere Varianten von Small-Subgroup-Angriffen. Allgemein beschrieben, bringt ein Angreifer das Opfer aktiv (z. B. Man-In-The-Middle) dazu, dass der geheime Schlüssel in einer kleinen Untergruppe der ausgehandelten Gruppe liegt. Damit kann der Angreifer den Schlüssel mit der erschöpfenden Suche finden [24, §2F].
Es ist jedoch aufwendig, die Anzahl von Element der Gruppe $E(\mathbb{F}_p)$ zu bestimmen. Die Ordnung wird daher approximiert nach dem Satz von Hasse berechnet [1, Formel 2.7]. Dieser besagt, dass die Ordnung der Gruppe $E(\mathbb{F}_p)$ im Bereich von $p$ liegt. Das heißt, diese ist annähernd gleich der Ordnung des Primkörpers. Muss $E(\mathbb{F}_p)$ aus Sicherheitsgründen eine bestimmte Anzahl von Elementen $2^n$ haben, muss $p$ mindestens $n$ Bit lang sein [2, S. 282]. Die in der Praxis genutzten Untergruppen besitzen die Ordnung, die nahezu genauso groß ist, die die Gruppenordnung, weswegen diese Abschätzung auch für die Base-Point-Untergruppe gilt.
Diskreter Logarithmusproblem über elliptische Kurven
Basierend auf der Tatsache, dass über eine elliptische Kurve eine Gruppe gebildet werden kann, lässt sich DLP für elliptische Kurven definieren. Hierbei kommt die Skalarmultiplikation zum Einsatz [2, Definition 9.2]:
$$ [k]P=P+P+...+P=T. $$
Wird die Punktverdopplung $k$ mal durchgeführt, so liegt das Ergebnis, wieder ein Punkt, auf der elliptischen Kurve. Da in $E(\mathbb{F}_p)$ die für die Addition benötigten Berechnung modulo $p$ erfolgen, ähnelt das Problem dem klassischen DLP, bei dem die Exponentiation ganzer Zahlen in $\mathbb{Z}_p$ stattfindet. Die Ergebnisse der Punktverdopplung liegen also wieder in der Menge $\mathbb{F}_p^2$ (Grundvoraussetzung für die Abgeschlossenheit gegenüber der betrachteten Verknüpfung).
In ECC wird der Punkt $P$ als öffentlich bekannter Parameter und das Ergebnis der Punktverdopplung $T$ als öffentlicher Schlüssel verwendet. Das Problem ist gelöst, wenn anhand der bekannten Werte der Parameter $k$ gefunden wird. Deshalb muss dieser geheim gehalten werden. Es ist bemerkenswert, dass die Anzahl der möglichen $k$-Werten der Ordnung der Untergruppe entspricht, die mit dem Base Point generiert wird. Der Base Point hat damit einen Einfluss auf den Schlüsselraum, da der Schlüssel basierend auf $k$ erzeugt wird.
Dabei ist die Berechnung von $T$ mit der additiven Version des Square-and-Multiply-Algorithmus, dem Double-and-Add-Algorithmus, effizient möglich [2, S. 283]. Andrerseits ist das Lösen des diskreten Logarithmus für ECP komplizierter als das diskrete Logarithmusproblem und das Faktorisierungsproblem. Für die letzteren existiert ein Algorithmus, der diese Probleme in subexponentieller Zeit lösen kann, -- der Index-Calculus-Algorithmus. Dabei ist die Laufzeit für das ECDLP-Problem mit gut ausgewählten endlichen Körper und elliptischen Kurven exponentiell [2, S. 287; 25]. Darüber hinaus übertrifft der Einsatz von ECC die auf RSA basierenden Verfahren in Bezug auf Betriebseffizienz [26, §7].
Allerdings benötigen generische DLP-Algorithmen, wie die Pollard-Rho- oder Baby-Step-Giant-Step-Methode, etwa $\sqrt{n}$ Schritte für einen erfolgreichen Angriff auf ECP, wobei $n$ die Ordnungen der verwendenden Untergruppe ist. Da bspw. das Mindestsicherheitsniveau $2^{80}$ Schritte ist, muss die Ordnung mindestens $2^{160}$ betragen. Daher muss die Primzahl $p$ die Mindestlänge von $160$ Bit haben [2, §9.4].
WPA3: Hintergrundwissen
Im zweiten Teil der WPA3-Serie wird das WPA3-Protokoll selbst vorgestellt. Besonderes Augenmerk wird auf das Dragonfly-Protokoll gelegt, durch das sich WPA3 von seinem Vorgänger abheben soll. Wie sich die hier dargelegten mathematischen Grundlagen der ECC in diesem Schlüsselvereinbarungsprotokoll widerspiegeln, wird ebenfalls im nächsten Artikel beleuchtet.
Dieser Artikel ist Teil einer schriftlichen Ausabreitung, die im Rahmen der IT-Security-Vertiefung "Spezielle Verfahren der IT-Sicherheit" bei Prof. Felke an der Hochschule Emden-Leer entstanden.
Appendix:
- $k$ kann nicht negativ sein $\Rightarrow k \geq 0$;
- $k$ kann nicht $0$ sein, da $[k]g = 0$ stets für $k = 0$, was im Grunde keine neue nützliche Information darstellt;
- $k < n+1$, da im schlechtesten Fall, wenn die Elemente $[s]a$ (für $1 \leq s \leq n, a \in G, \text{#}G=n$) verschieden sind,
jedes weitere Element $[n+1]a$ ein in der Gruppe vorhandenes Element darstellt.
Das heißt, das neutrale Element befindet sich bereits unter den Elementen $[s]a$, für $1 \leq s \leq n$.
Quellen:
- Bundesamt für Sicherheit in der Informationstechnik, Elliptic curve cryptography. (2018)
- Paar, C. und Pelzl, J. Kryptografie verständlich (2016)
- BlueKrypt cryptographic key length NIST recommendations (2020)
- Wolfram Mathworld, Elliptic curves.
- Bitcoin Wiki, Secp256k1.
- Bitcoin Wiki, Wie funktioniert Bitcoin?
- Blair, M. How does ECDSA work in Bitcoin
- Cryptography Stack Exchange, Why do the discriminant and primality of the group order of an elliptic curve affect security?
- Cryptography Stack Exchange, Why are singular "elliptic" curves bad for crypto?
- Karpfinger, C. and Meyberg, K. Algebra: Gruppen - Ringe - Körper (2010)
- Lang, H. W. Gruppentheorie (2018)
- Chavez, A. and O’Neill, C. The fundamental theorem of finite fields: A proof from first principles (2021)
- Universität Kiel, Skript Mathematik für Informatiker (2012)
- Nakov, S. Practical cryptography for developers (2018)
- Wolfram Mathworld, Elliptic discriminant
- rfc6090 (2011)
- Silverman, J.H. An introduction to the theory of elliptic curves
- Neal, A. Elliptic curves group law
- Lynn, B. Group of Points.
- Cryptography Stack Exchange. In Elliptic Curve, what does the point at infinity look like?
- Trustica. Elliptic curves: point at infinity in the projective plane
- Herong, Y. Infinity point on an elliptic curve
- Clarke, D. and Hao, F. Cryptanalysis of the dragonfly key exchange protocol (2013)
- Valenta, L. et al. Measuring small subgroup attacks against diffie-hellman (2016)
- Petit, C. Elliptic curve cryptography
- Mahto, D. and Yadav, D.K. Performance analysis of RSA and elliptic curve cryptography (2018)